Mit diesen kostenlosen Online-Rechner können Sie einfach und schnell Dezimalzahlen in Binärzahlen umwandeln.
Bewerten Sie diesen Konverter
So verwenden Sie den Dezimal-Binär Konverter
Zeit benötigt: 1 Minute
- Eingabe der Dezimalzahl
Geben Sie eine Dezimalzahl in das erste feld ein
- Drücken Sie die „Konvertieren“ Schaltfläche
Drücken Sie die Schaltfläche „Konvertieren“ unterhalb des Zahlenfeldes
- Überprüfen Sie das Ergebnis
Die Binärzahl wird im zweiten Feld angezeigt
- Kopieren oder Sichern
Optional können Sie die Ausgabe in die Zwischenablage kopieren oder als Datei auf ihrem Gerät speichern
Funktionen des Konverters
| 🔢Dezimal Eingabelänge: | Bis zu 7 Ziffern |
| ⚡Umwandlungsgeschwindigkeit | Sofort! |
| ➡️Binäre Ausgabe: | Anzeigen, Kopieren, Sichern |
| 🎯Umrechnungsgenauigkeit: | 100% |
Lesen (oder sehen) Sie sich unser Tutorial über die Umrechnung von Dezimal- in Binärzahlen an, um mehr über den Prozess der Umwandlung von Dezimalzahlen in Binärzahlen zu erfahren.
Testen Sie auch den Binär-Dezimal-Konverter!
Umrechnung von Dezimal in Binär
Wenn Sie mit Computern arbeiten, benötigen Sie vielleicht ein Grundwissen über das binäre Zahlensystem. Vielleicht möchten Sie aber auch nur zum Spaß das Binärsystem kennenlernen. In beiden Fällen kann es nützlich sein, zu wissen, wie man vom Dezimalzahlensystem in das Binärzahlensystem konvertiert.
Und das Beste daran ist, dass man dafür weder einen Abschluss in Mathematik noch einen Dezimal-/Binärrechner benötigt.
Einsen und Nullen
Binär ist die Sprache, die Computer sprechen. Sie setzt sich aus einer Reihe von Einsen und Nullen zusammen. Auf den ersten Blick mag das wie Unsinn aussehen, aber es gibt eine Methode dafür. Wir beginnen mit einer einfachen, einstelligen Zahl und erklären, wie man eine Dezimalzahl in eine Binärzahl umwandeln kann. Nehmen wir die Zahl 7.
Bei der Umwandlung von Dezimal- in Binärzahlen muss die Zahl, die Sie umwandeln möchten, neu definiert werden. 7 kann einfach als 7 oder auch als 4+3 dargestellt werden. Die Umschreibung der Zahl ist der erste Schritt bei der Umwandlung in das Binärsystem. Das Wichtigste ist, dass wir unsere Dezimalzahl in die Summe der Potenzen von 2 zerlegen.
Betrachten wir also die Zahl 7 und die Potenzen von 2. Welche Potenz von 2 kommt der Zahl 7 am nächsten und ist gleichzeitig gleich oder kleiner als 7?
2² ergibt 4, also beginnen wir mit 4, um 7 zu zerlegen. Wir müssen 3 addieren, um den Rest von 7 zu bilden. Jetzt können wir also 7=4+3 betrachten.
Es kann hilfreich sein, eine Tabelle mit Potenzen von 2 als Referenz zu haben. Wir haben einen Teil der Tabelle in das Bild unten eingefügt.

Jetzt haben wir 3, aber es gibt keine Potenzen von 2, die 3 ergeben. Wir müssen 3 auf die gleiche Weise zerlegen wie die 7. Lass uns also die Summe der 2er-Potenzen finden, die 3 ergibt. Denken Sie daran, dass wir mit Potenzen von 2 gleich oder kleiner als 3 beginnen müssen. 2¹ ergibt 2, und 20 ergibt 1.

Wir haben in diesem Beispiel drei verschiedene Potenzen von 2 verwendet. Die binäre Darstellung von 7 ist also drei Ziffern lang. Da die höchste Potenz von 2, die wir benötigen, 2² war, beginnen wir damit, zu zählen, wie oft 2² verwendet wurde. In der Binärdarstellung kann es nur zwei Antworten auf diese Frage geben: Sie wurde ein- oder null Mal verwendet. Wenn wir es verwendet haben, geben wir eine 1 an, wenn nicht, eine 0.
Die Verwendung von 2² bedeutet, dass wir eine 1 notieren. Jetzt arbeiten wir abwärts und zählen die restlichen Potenzen von 2, die wir verwendet haben. Wir haben 2¹ verwendet, also notieren wir eine weitere 1. Wir haben auch 20 verwendet, also notieren wir an der letzten Stelle ebenfalls eine 1.
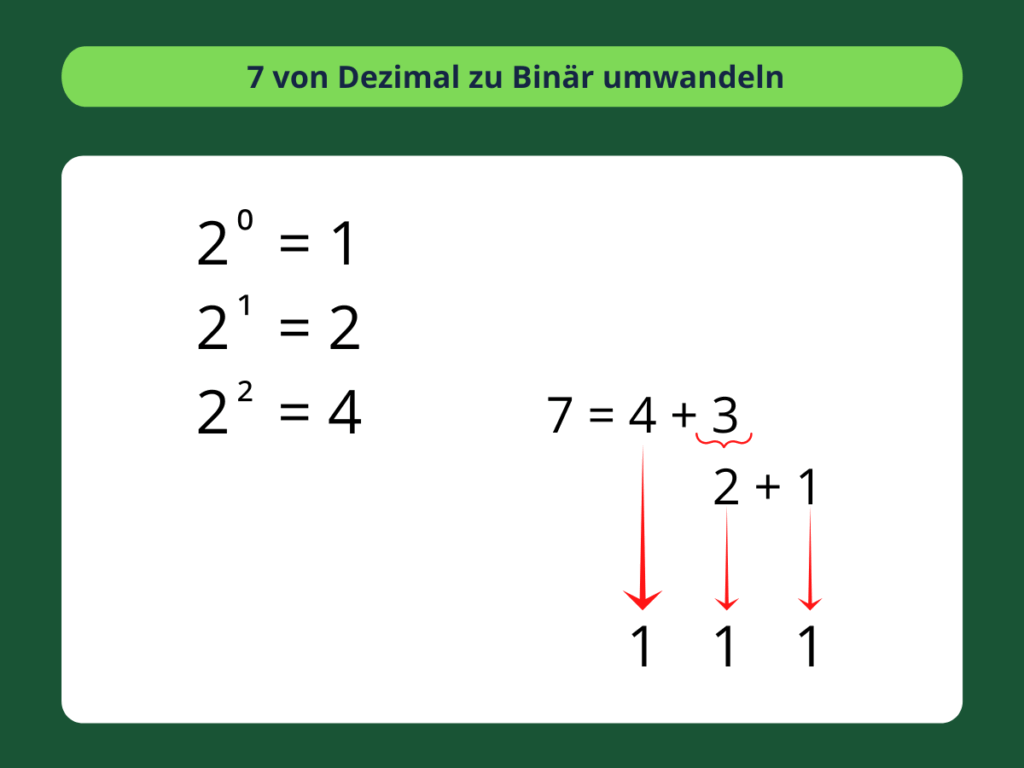
Jetzt haben wir die dezimale 7 in die binäre Form 111 umgewandelt.
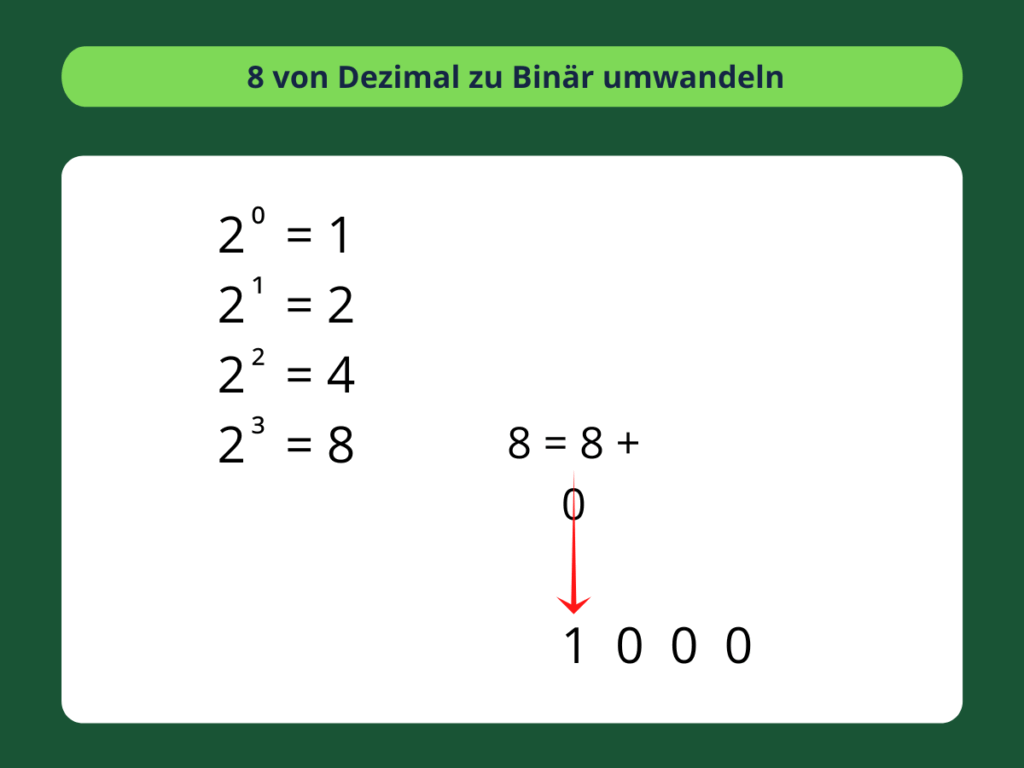
Wir können die 8 als noch einfacheres Beispiel für die Umwandlung von Dezimal- in Binärzahlen verwenden. Welche Potenz von 2 ist gleich oder kleiner als 8? 2³ ergibt genau 8. Wir brauchen also nichts zu zerlegen.
Wir haben 2³ einmal verwendet. Wir haben 2², 2¹ und 20 null Mal verwendet. 8 ergibt also 1000 in binärer Form. Beim Binärsystem wird einfach gezählt, wie oft eine 2er-Potenz verwendet wurde, um das Dezimalsystem zu zerlegen.
Bedeutet das, dass wir, wenn wir die Dezimalzahl 78 binär schreiben wollen, die binären Entsprechungen in jeder Ziffer kombinieren können? 111 und 1000? Nun, nicht ganz. 1111000 wird zu 120! Aber wenn wir 78 in Binärzahlen umwandeln wollen, ist es so einfach wie die Umwandlung eines einzelnen Dezimalwertes.
Wie zuvor schauen wir uns an, welche Potenz von 2 am nächsten an 78 liegt. 26 ergibt 64, was 78 am nächsten kommt, ohne 78 zu überschreiten. Wir können 78 umdefinieren als 78 = 64 + 14.

Jetzt müssen wir auch 14 umdefinieren. Wir können 2³ verwenden, um 8 zu erhalten, und jetzt müssen wir 6 addieren, um 14 zu erhalten. Da 6 auch kein Bestandteil von 2 ist, muss sie in eine Summe von Potenzen von 2 zerlegt werden.
Zum Glück gibt es 2² die Zahl 4 und 2¹ die Zahl 2. Jetzt müssen keine weiteren Zahlen mehr zerlegt werden, und wir können sie in binäre Zahlen umwandeln. Da wir bei 26 angefangen haben, müssen wir uns fragen, ob wir diese Potenz und jede davor liegende Potenz bis 20 verwendet haben.
Wie oft haben wir 26 verwendet? 1
Wie oft haben wir 25 verwendet? 0
Wie oft haben wir 24 verwendet? 0
Wie oft haben wir 2³ verwendet? 1
Wie oft haben wir 2² verwendet? 1
Wie oft haben wir 2¹ verwendet? 1
Wie oft haben wir 20 verwendet? 0
78 in Binärformat ist also 1001110

Nicht so schlimm, wie Sie dachten oder? Der gleiche Algorithmus funktioniert für dreistellige Dezimalzahlen und mehr. Der einzige Unterschied besteht darin, dass Sie möglicherweise eine umfangreichere Tabelle mit Potenzen von 2 (oder einen Taschenrechner) benötigen, um die Gleichung zu berechnen. Oder Sie verwenden für größere Zahlen einen Dezimal-Binär-Konverter, wie den oben auf dieser Seite. Unterm Strich ist die Umwandlung von Dezimal-in Binärzahlen so einfach wie 1, 2, 3 – oder sagen wir 1, 10, 11!
Tabelle der ersten hundert Dezimalzahlen in binärer Form
In der folgenden Tabelle sind die Dezimalzahlen von 0 bis 100 zusammen mit ihrer binären Darstellung angeführt.
| Decimal | Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 33 | 100001 |
| 34 | 100010 |
| 35 | 100011 |
| 36 | 100100 |
| 37 | 100101 |
| 38 | 100110 |
| 39 | 100111 |
| 40 | 101000 |
| 41 | 101001 |
| 42 | 101010 |
| 43 | 101011 |
| 44 | 101100 |
| 45 | 101101 |
| 46 | 101110 |
| 47 | 101111 |
| 48 | 110000 |
| 49 | 110001 |
| 50 | 110010 |
| 51 | 110011 |
| 52 | 110100 |
| 53 | 110101 |
| 54 | 110110 |
| 55 | 110111 |
| 56 | 111000 |
| 57 | 111001 |
| 58 | 111010 |
| 59 | 111011 |
| 60 | 111100 |
| 61 | 111101 |
| 62 | 111110 |
| 63 | 111111 |
| 64 | 1000000 |
| 65 | 1000001 |
| 66 | 1000010 |
| 67 | 1000011 |
| 68 | 1000100 |
| 69 | 1000101 |
| 70 | 1000110 |
| 71 | 1000111 |
| 72 | 1001000 |
| 73 | 1001001 |
| 74 | 1001010 |
| 75 | 1001011 |
| 76 | 1001100 |
| 77 | 1001101 |
| 78 | 1001110 |
| 79 | 1001111 |
| 80 | 1010000 |
| 81 | 1010001 |
| 82 | 1010010 |
| 83 | 1010011 |
| 84 | 1010100 |
| 85 | 1010101 |
| 86 | 1010110 |
| 87 | 1010111 |
| 88 | 1011000 |
| 89 | 1011001 |
| 90 | 1011010 |
| 91 | 1011011 |
| 92 | 1011100 |
| 93 | 1011101 |
| 94 | 1011110 |
| 95 | 1011111 |
| 96 | 1100000 |
| 97 | 1100001 |
| 98 | 1100010 |
| 99 | 1100011 |
| 100 | 1100100 |
Fragen und Antworten zur Umwandlung von Dezimal in Binär
Der Dezimal-zu-Binär-Konverter auf de.ConvertBinary.com ist wirklich einfach zu bedienen.
Folgen Sie einfach diesen Schritten: Geben Sie eine Dezimalzahl in das erste Feld ein und klicken Sie dann auf die Schaltfläche „Konvertieren“
Die Binärdarstellung Ihrer Dezimalzahl wird sofort im Feld darunter angezeigt.
Um Dezimalzahlen in ihr binäres Format umzuwandeln, haben Sie zwei Möglichkeiten: Sie können entweder einen Online-Konverter verwenden (wie den kostenlosen von de.ConvertBinary.com), oder Sie können es manuell tun.
Wenn Sie lernen möchten, wie man Dezimalzahlen manuell in Binärzahlen umwandelt, können Sie diese Anleitung lesen oder sich das dazugehörige Tutorial ansehen.
Der Konverter nimmt die Dezimalzahl und betrachtet die Potenzen von 2. Es findet die Potenz von 2, die der Dezimalzahl am nächsten kommt und gleichzeitig gleich oder kleiner als die Dezimalzahl selbst ist.
Dann wird der Vorgang so lange wiederholt, bis kein Rest mehr übrig bleibt.
Der Prozess läuft automatisch ab und ist so schnell, dass es sich anfühlt, als würde er sofort ausgeführt werden, selbst bei großen Zahlen.
Ja natürlich! Wenn Sie eine binäre Zahl in ihre dezimale Form umwandeln möchten, können Sie den Binär-Dezimal-Konverter auf de.ConvertBinary.com verwenden.
Die Zahl 10 (Zehn) ist 1010 (Eins-Null-Eins-Null) in Binär.
Eine Tabelle mit den Binärdarstellungen der Dezimalzahlen von 0 bis 100 finden Sie unter de.ConvertBinary.com
