Mit diesem Binär-Dezimal-Konverter können Sie ganz einfach und rasch Binärzahlen in Dezimalzahlen umwandeln.
Bewerten Sie den Konverter
So verwenden Sie den Binär zu Dezimal Konverter
Zeit benötigt: 1 Minute
- Binärzahleingabe
Geben Sie im ersten Feld eine Binärzahl ein.
- Drücken Sie die „Konvertieren“ Schaltfläche
Drücken Sie unter dem Feld für die Binärzahl die Schaltfläche „Konvertieren“.
- Überprüfen Sie das Ergebnis
Das Ergebnis der Dezimalzahl erscheint im zweiten Feld.
- Kopieren oder Sichern
Optional, können Sie das Ergebnis in die Zwischenablage kopieren oder als Datei auf Ihrem Gerät sichern.
Eigenschaften des Konverters
| 🔟 Binärcode Eingabelänge: | Bis zu 25 Ziffern |
| ⚡ Umwandlungsgeschwindigkeit: | Sofort! |
| ➡️ Dezimale Ausgabe: | Anzeigen, Kopieren, Sichern |
| 🎯Umrechnungsgenauigkeit: | 100% |
Lesen (oder sehen) Sie sich unser Tutorial über die Umwandlung von Binär- in Dezimalzahlen an, um mehr über den Umwandlungsprozess von Binär- in Dezimalzahlen zu erfahren.
Probieren Sie auch den Dezimal-Binär-Konverter aus!
Umwandlung von Binär in Dezimal
Möchten Sie erfahren, wie man Binärzahlen in Dezimalzahlen umwandelt? All diese Einsen und Nullen können auf den ersten Blick recht abschreckend wirken. Hier finden Sie einen Umrechnungskonverter von Binär- in Dezimalzahlen, oder Sie können den Umrechnungsprozess auch gerne selbst erlernen – ganz ohne Computer.
Wenn Sie dachten, dass für die Umrechnung von Binär- in Dezimalzahlen komplizierte Formel erforderlich wären, können Sie jetzt etwas aufatmen. Um vom binären Zahlensystem in das dezimale Zahlensystem umzuwandeln, müssen Sie eigentlich nur drei Dinge wissen. Erstens: Denken Sie daran, dass die Einsen und Nullen, aus denen das Binärsystem besteht auf eine Ja- oder Nein-Frage basiert. Eine Eins steht für „Ja“, die Null für „Nein“. Als nächstes, wenn Sie die Potenzen von 2 kennen, wird alles andere ein Kinderspiel werden. Der letzte Schritt besteht aus einfacher Addition.
Die (Super-)Potenzen der 2
Wir können uns bei den Potenzen von 2 dafür bedanken, dass dies so einfach ist. Sollten Sie damit noch nicht vertraut sein, erleichtert Ihnen eine dafür erstellte Tabelle die Arbeit zusätzlich. Sie brauchen jedoch keine umfangreiche Tabelle, es sei denn, Sie möchten sehr große Binärzahlen konvertieren. Wenn die zu konvertierende Binärzahl zum Beispiel dreistellig ist, brauchen Sie dabei nur die ersten drei Potenzen von 2 (20 , 2¹, and 2²).
Betrachten wir eine dreistellige Binärzahl, 101.

Um die Binärzahl 101 in eine Dezimalzahl umzuwandeln, müssen wir die ersten drei Potenzen von 2 verwenden. Die einfachste Art, sich das vorzustellen ist, die Binärzahl aufzuschreiben und darüber die Potenzen von 2 einzutragen. Denken Sie daran, dass Sie bei 20 auf der rechten Seite beginnen und sich nach links weiterarbeiten, bis Sie keine Binärziffern mehr haben.

Wir haben 1, 0 und 1 und eine Potenz von 2 für jede Binärziffer. Wir beginnen mit der Ziffer ganz rechts, dem kleinsten bedeutsamen Wert (Least Significant Bit – LSB): Schauen Sie sich 20; was steht unterhalb? Eine Eins. Das bedeutet, dass wir 20 in der dezimalen Auswertung verwenden werden.
Arbeiten wir uns jetzt weiter bis zur Ziffer ganz links. Was steht unter 2¹? Eine Null. Das bedeutet, dass wir 2¹ nicht verwenden werden. Und unter 2²? Noch eine Eins. Um herauszufinden, was 101 in Dezimalzahlen ist, brauchen wir 20 and 2².

Der Rest ist ganz einfach – 20 und 2² sind 1 bzw. 4. Jetzt addiere einfach 1 + 4. Die Binärzahl 101 ist die dezimale 5.
Vergessen Sie nicht, dass Sie immer von rechts nach links vorgehen, also vom niedrigsten Wert (LSB, die Ziffer ganz rechts) zum höchstwertigen Wert (MSB, die Ziffer ganz links).

Es ist unglaublich einfach, wenn Sie sich 1 als „Ja“ und 0 als „Nein“ vorstellen können. Größere Zahlen funktionieren genauso. Werfen wir ein paar zusätzliche Nullen in den Mix und verwenden 100001. Das ist zwar lang, aber die Methode ist identisch. Diesmal benötigen wir nur 6 Potenzen von 2, eine für jede Ziffer der Binärzahl.
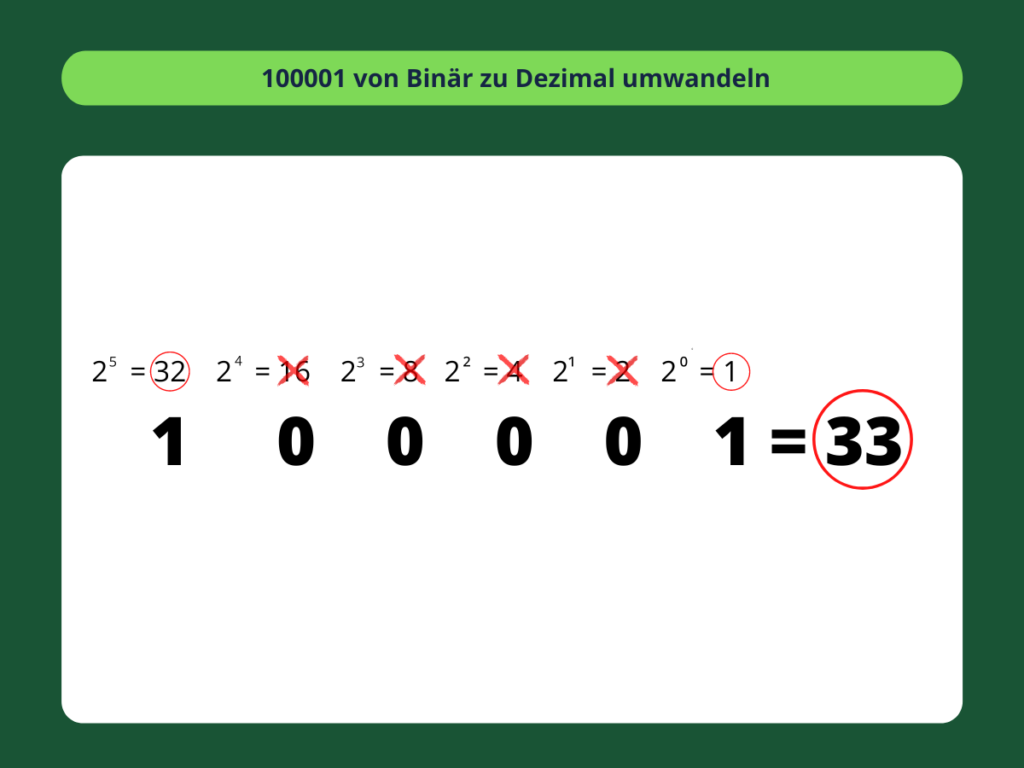
Welche Potenzen von 2 entsprechen einer Eins? Nur 26 und 20. Nun addieren wir diese 2er-Potenzen zusammen. 100001 als Dezimalzahl ist 33.
Um zu zeigen, wie einfach die Umwandlung von Binär- in Dezimalzahlen ist, nehmen wir eine noch längere Binärzahl: 11001100. Für diese Umrechnung müssen wir bis zur 27 gehen.
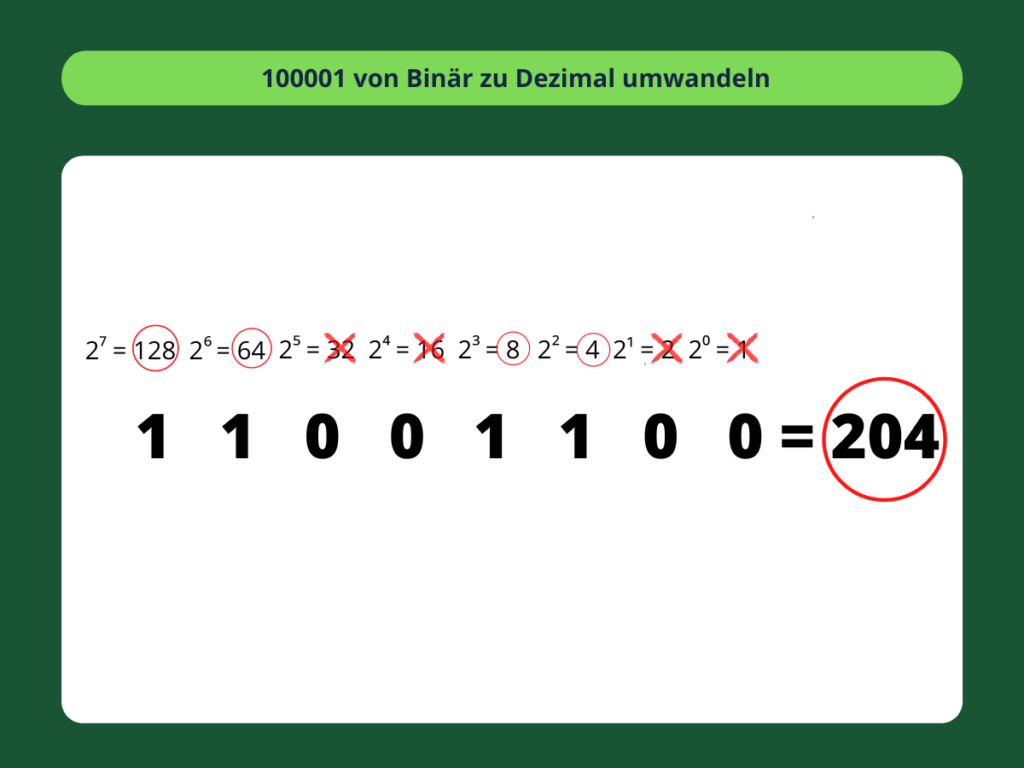
Alles, was wir jetzt noch tun müssen, ist die verwendeten 2er-Potenzen zu addieren. Denken Sie daran, dass wir sie nur „benutzen“, wenn sie einer Eins entsprechen. In diesem Fall müssen wir 128, 64, 8 und 4 addieren, um die Dezimalzahl ermitteln zu können. Alles andere wird durch eine Null angezeigt wodurch wir sie nicht berücksichtigen brauchen. 11001100 in Binärform ist die Dezimalzahl 204.
Wenn Sie selbst ausprobieren möchten, können Sie den Binär-Dezimal-Rechner auf dieser Seite verwenden, um Ihr Ergebnis zu kontrollieren. Üben Sie ein paar Mal, und Sie werden die Sprache der Computer mit Leichtigkeit sprechen.
Tabelle der ersten hundert Binärzahlen in dezimaler Darstellung
In der folgenden Tabelle sind die Binärzahlen von 0 bis 1100100 zusammen mit ihrer Dezimaldarstellung angeführt.
| Binär | Dezimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| 10011 | 19 |
| 10100 | 20 |
| 10101 | 21 |
| 10110 | 22 |
| 10111 | 23 |
| 11000 | 24 |
| 11001 | 25 |
| 11010 | 26 |
| 11011 | 27 |
| 11100 | 28 |
| 11101 | 29 |
| 11110 | 30 |
| 11111 | 31 |
| 100000 | 32 |
| 100001 | 33 |
| 100010 | 34 |
| 100011 | 35 |
| 100100 | 36 |
| 100101 | 37 |
| 100110 | 38 |
| 100111 | 39 |
| 101000 | 40 |
| 101001 | 41 |
| 101010 | 42 |
| 101011 | 43 |
| 101100 | 44 |
| 101101 | 45 |
| 101110 | 46 |
| 101111 | 47 |
| 110000 | 48 |
| 110001 | 49 |
| 110010 | 50 |
| 110011 | 51 |
| 110100 | 52 |
| 110101 | 53 |
| 110110 | 54 |
| 110111 | 55 |
| 111000 | 56 |
| 111001 | 57 |
| 111010 | 58 |
| 111011 | 59 |
| 111100 | 60 |
| 111101 | 61 |
| 111110 | 62 |
| 111111 | 63 |
| 1000000 | 64 |
| 1000001 | 65 |
| 1000010 | 66 |
| 1000011 | 67 |
| 1000100 | 68 |
| 1000101 | 69 |
| 1000110 | 70 |
| 1000111 | 71 |
| 1001000 | 72 |
| 1001001 | 73 |
| 1001010 | 74 |
| 1001011 | 75 |
| 1001100 | 76 |
| 1001101 | 77 |
| 1001110 | 78 |
| 1001111 | 79 |
| 1010000 | 80 |
| 1010001 | 81 |
| 1010010 | 82 |
| 1010011 | 83 |
| 1010100 | 84 |
| 1010101 | 85 |
| 1010110 | 86 |
| 1010111 | 87 |
| 1011000 | 88 |
| 1011001 | 89 |
| 1011010 | 90 |
| 1011011 | 91 |
| 1011100 | 92 |
| 1011101 | 93 |
| 1011110 | 94 |
| 1011111 | 95 |
| 1100000 | 96 |
| 1100001 | 97 |
| 1100010 | 98 |
| 1100011 | 99 |
| 1100100 | 100 |
Fragen und Antworten zur Umwandlung von Binär- in Dezimalzahlen
Den Binär-Dezimal-Konverter von de.ConvertBinary.com ist wirklich einfach zu bedienen.
Folgen Sie einfach diesen Schritten: Geben Sie Ihre Binärzahl in das erste Feld ein und klicken Sie dann auf die Schaltfläche „Umrechnen“.
Die dezimale Darstellung Ihrer Binärzahl wird sofort im Feld darunter angezeigt.
Um Binärzahlen in ihre dezimale Form zu konvertieren, haben Sie zwei Möglichkeiten: Sie können entweder einen Online-Konverter verwenden (wie den kostenlosen von de.ConvertBinary.com), oder Sie können es manuell tun.
Wenn Sie lernen möchten, wie man Binärzahlen manuell in Dezimalzahlen umwandelt, können Sie diese Anleitung lesen, oder sich das zugehörige Tutorial ansehen.
Sie verwendet eine Skriptfunktion, die die Eingabe (in unserem Fall die Binärzahl) analysiert und eine vollständige Dezimalzahl zurückgibt.
Der Funktionsaufruf gibt an, dass das Binärsystem verwendet werden soll.
Der Prozess läuft automatisch ab und ist so schnell, dass es sich anfühlt, als würde es sofort gehen, selbst bei sehr großen Zahlen.
Selbstverständlich! Wenn Sie eine Dezimalzahl in eine Binärzahl umwandeln möchten, können Sie den Dezimal zu Binär Konverter auf de.ConvertBinary.com verwenden
Die Binärzahl 1000 (Eins-Null-Null-Null) ist 8 (Acht) im Dezimalsystem.
Eine Tabelle mit den Binärdarstellungen der Dezimalzahlen von 0 bis 100 finden Sie unter de.ConvertBinary.com.
